蝠猫学算法#3——算法效率度量

文章寄语

mi promesas trovi vin,do ankaŭ vi, bonvolu ne plu dubu.(我一定会找到你，所以也请你，不要再怀疑。)
　　　　　　　　　　　　　　　　　　　　—— <<星灵感应>>

---

引言

数据结构笔记第三篇。算法效率的度量[考纲有此内容]

知识点大致按照《Hello!算法》书籍进行。因为数据结构与算法在非常多的考试中都有。

本人基础较弱，可能会有许多错误，恳请批评指正。

下面是几个上述提到的链接：

《Hello!算法》网页版 全国计二级官网 洛谷官网-刷题可用

星空如此灿烂，灯塔与之响应。出发吧

---

第三节 时间和空间复杂度

时间复杂度

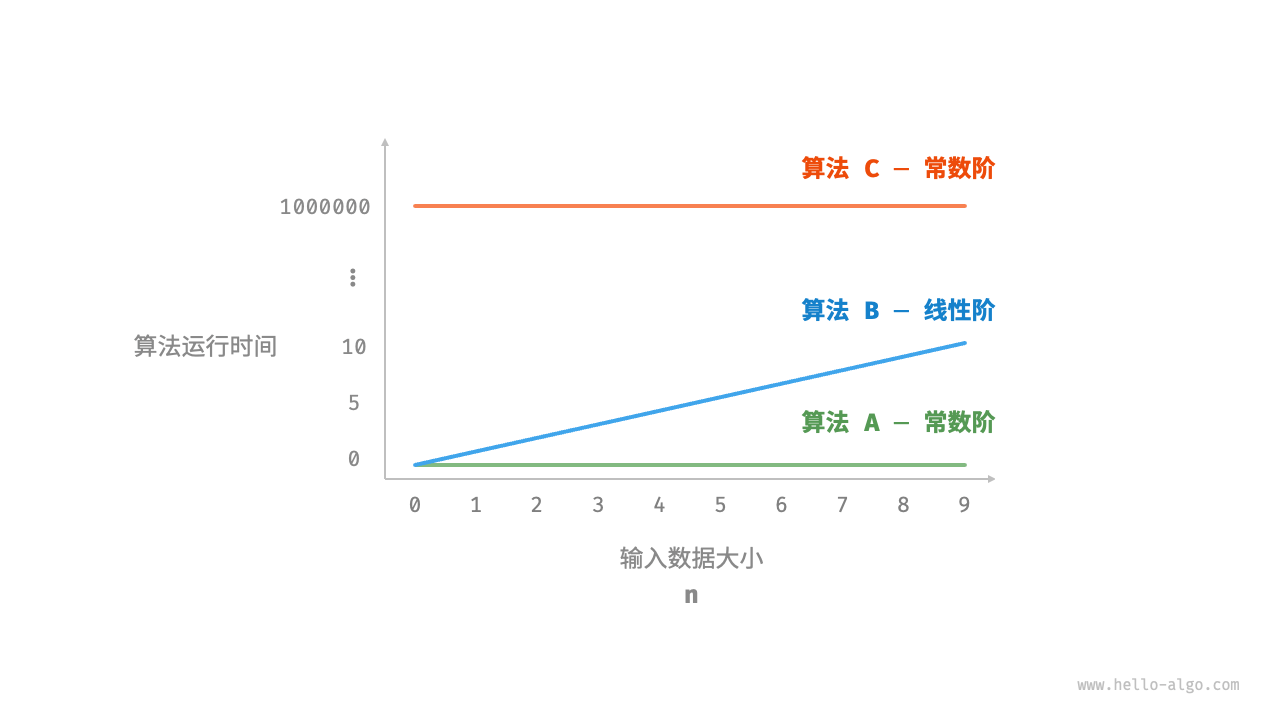
时间增长趋势

时间复杂度评估代码的运行时间。

比如现在我有三个循环，A只循环一次，B循环n次，C循环1000次。怎么判断这三者的时间复杂度？

很简单，可以使用高数中极限的概念理解 ，具体如下：

• A的时间复杂度为: 极限结果不受n影响，不管n取多少都是1，称之 “常数阶” 复杂度。
  
• B的时间复杂度为: 极限结果受n影响，n取值越大结果就越大，称之 “线性阶” 复杂度。
  
• C的时间复杂度为: 极限结果不受n影响，不管n取多少都是1000，称之 “常数阶” 复杂度。
  

这里就可以看到，只要n的取值大于1000，常数阶复杂度一定优于线性阶。同时AC复杂度其实相同。

函数渐进上界

书里那个什么渐进上界我看不明白，我还以为是高数里函数有界性的那个上界。但是没看懂不要紧。

只需要明白复杂度的符号是一个大O即可。然后针对特定代码，就像下面这段：

void algorithm(int n) {
    //以下语句一共操作了3次
    int a = 1;  
    a = a + 1;  
    a = a * 2;  
    //一次循环均有i++和输出操作，一共2n次
    for (int i = 0; i < n; i++) { 
        cout << 0 << endl;  
    }
}

所以这段代码一共操作了次,操作数用T(n)表示，所以操作数一共是:

然后使用极限，因为趋于无穷，可以看成这样：

极限中斜率最大的函数占优势。所以时间复杂度为

因为系数c = 2不确定，他可以取任意大小，舍弃。最终的结果为 ,即”线性阶”复杂度。

例拿上面的[2n+3]举例，总有这个式子成立：

这个叫上界函数。这不就是前面所提到的函数有界性吗？

函数渐进上界定义

若存在正实数和实数,使得对于所有的,均有，则可认为给出了的一个渐近上界,记为

函数渐进上界图像

其实还可以用函数极限：

这里，函数的渐进上界为

函数极有界结果必然存在。所以抓出的最高次项，然后去掉系数即可。

若有一个函数它的总操作次数为，那么这个函数的渐进上界就为。

在n趋向于无穷时，总有成立。因为系数忽略不计，所以它的时间复杂度为。即”平方阶”复杂度.

时间推算方法

函数增长趋势，也就是斜率。不会受系数c和加减常数影响。

推算方法回顾:

• 忽略所有常数。
• 忽略所有系数。
• 嵌套使用乘法，顺序使用加法。
• 在操作数趋向于无穷时进行比较。

img

在操作数趋向于无穷时，复杂度从低到高分别为：常数阶 < 对数阶 < 线性阶 < 线性对数阶 < 平方阶 < 指数阶 < 阶乘阶。

常见复杂度类型

1. 常数阶

操作数大小与其无关，始终是一个固定的常数。复杂度最小，代码此时最优。

*哈希表的增删查均为O(1)*

2. 线性阶

常见于循环遍历的情况，没有嵌套。复杂度为。

与操作数大小有关，操作数越大耗时越多。复杂度比常数阶高。

*根据实际输入或数组/链表的规模决定*

3. 平方阶

常见于嵌套，两层即n(n) ->,三层即n(n(n)) ->。实际上复杂度是,α是层数。

嵌套计算用乘法，比如内层循环是, 外层循环是。操作数即为.

因为系数c和常数均可省略，结果为。比线性阶耗时更多，更复杂。

*根据实际输入或数组/链表的规模决定*

4. 指数阶

指数爆炸！类似于细胞分裂。所以操作总数为: (递归树的总节点数)

• 等比数列求和公式:

等比数列求和的结果为,因为首项不符合等比数列补加上，最终为

因为指数爆炸的特性，应当避免使用指数阶复杂度。

*多在递归和穷举法中使用。数据量较小时可以使用*

5. 对数阶

常见于分治。不管操作数是多少，步数均为 (看能除多少个2)后 +1。即，最终复杂度为。

因为换底公式，底数可以随意转换。所以底数2相当于系数c，可以省略。即复杂度为。

*多在分治中使用。仅次于常数级复杂度。优秀的复杂度*

6. 线性对数阶

常见于线性阶和对数阶嵌套的情况。嵌套用乘法，即最终为。

*多在主流排序算法中使用。非常优秀的复杂度*

7. 阶乘阶

常见于解决”数字全排列”问题。因为嵌套计算用乘法。所以操作总数为:

我用以下例子来表明指数阶和阶乘阶的区别：

• 当规模n取20时，指数阶的操作数为
• 当规模n取20时，阶乘阶的操作数为

*比指数爆炸还恐怖的存在*

最差/最佳/平均时间复杂度

在前面函数渐进上界提到过，关于

的复杂度必须存在，且极限存在必定有界。有界是两个界，有渐进上界，肯定有渐进下界。

上界指某个值时函数图像上所有点都小于这个值，相当于下限，也就是最坏情况下的操作数。称作最差时间复杂度，记为。

相反下界指在某个值时函数图像上所有点都大于这个值，相当于上限，也就是最佳情况下的操作数。称作最佳时间复杂度，记为。

空间复杂度

代码空间和推算方法

时间复杂度看输入，空间复杂度只看开辟了多少空间。用了多少空间，返回了多少空间。由暂存数据、栈帧空间和输出数据组成。图片如下:

算法空间

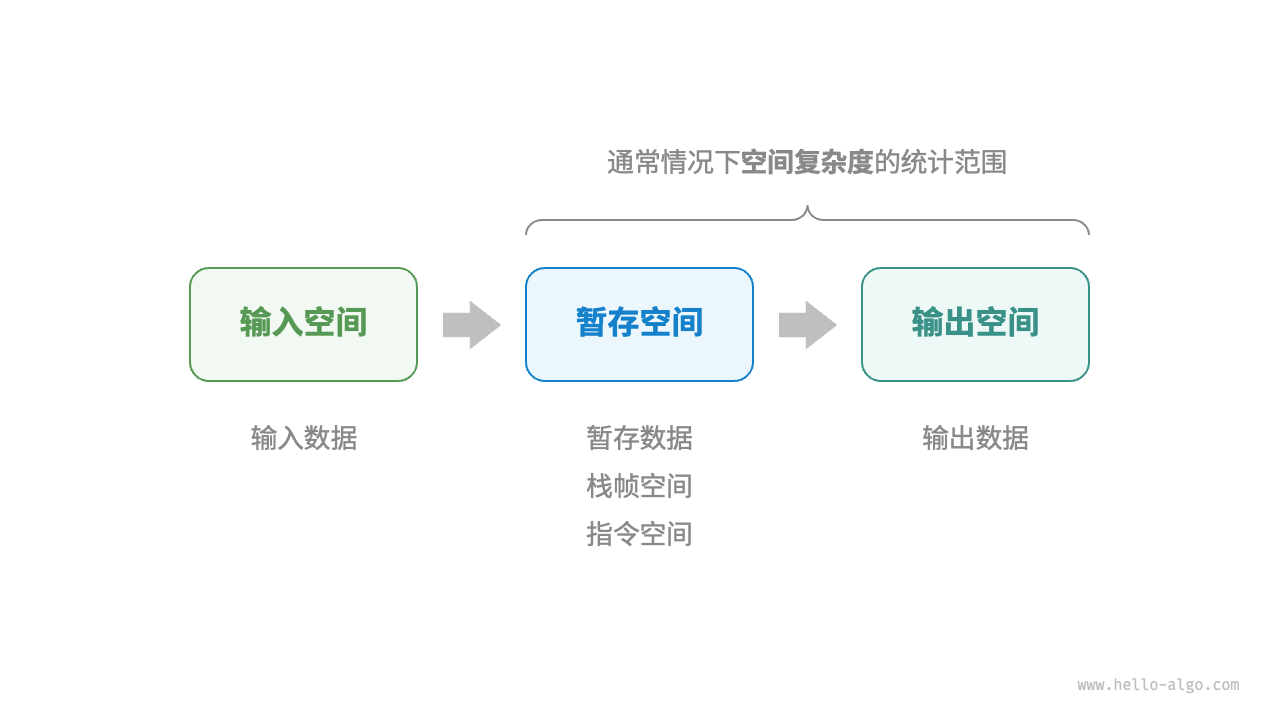
原地算法指在原来的基础上操作，不使用辅助空间。即常数阶。

int func() {
    return 0;
}
/* 循环的空间复杂度为 O(1) */
void loop(int n) {
    for (int i = 0; i < n; i++) {
        func();
    }
}
/* 递归的空间复杂度为 O(n) */
void recur(int n) {
    //直到n=1之前都不返回return
    if (n == 1) return;
    return recur(n - 1);
}

递归函数需要统计栈帧空间,我的理解就是判断每一层是否已经返回值。一次循环如果已经返回值了，释放空间。就和流水线后装满产品的箱子会被运走一样。

常见复杂度类型

从低到高，空间复杂度类型为常数阶 < 对数阶 < 线性阶 < 平方阶 < 指数阶

1. 常数阶

一次循环如果已经返回值了，会释放空间。不会积累。空间最优。

*常见于和n无关的东西，有返回值的调用等。与循环几次无关。*

2. 线性阶

一次循环后若当前未返回值，一次需要算一次。数组,列表,栈,队列,哈希表等，开多少就占多少。所以创建这类对象就是线性阶

*常见于和n有关的东西*

3. 平方阶

常见于递归嵌套的复杂度。在嵌套时，省略系数c，即复杂度为。

*常见于和n有关的东西，并且以嵌套形式存在*

4. 指数阶

用斐波那契的例子来看，并按前文的等比数列求和公式，求出这棵二叉树应该一共要开个位置。带入情景即指数阶复杂度。

*常见于二叉树，使用二叉树来帮助理解*

5. 对数阶

空间仅次于常数阶。不过形成了 (看能除多少个2)层的递归树，深度多少就使用了多少空间。忽略底数即复杂度为

*常见于递归二叉树，用递归二叉树来帮助理解*

平衡空间/时间

人们总是希望空间复杂度和时间复杂度都是最低最佳，但是很多情况不可能同时优化，只能优化其中的一个。

所以这种就得具体问题具体分析，有”空间换时间”策略和”时间换空间”策略两种策略。但是因为时间更宝贵，所以一般都用”空间换时间”策略。

---

总结

文章结语

人类把最精密的保密系统，都用在了自我毁灭上。
　　　　　　　　　　　　　　　　　　　　——流浪地球2

---

笔记完毕 编辑完毕时间CST 6.30 01:10

最后修改于8.15 23:15